معرفی شرکت ها
bpl-0.1.1
تبلیغات ما
مشتریان به طور فزاینده ای آنلاین هستند. تبلیغات می تواند به آنها کمک کند تا کسب و کار شما را پیدا کنند.
مشاهده بیشتر
تبلیغات ما
مشتریان به طور فزاینده ای آنلاین هستند. تبلیغات می تواند به آنها کمک کند تا کسب و کار شما را پیدا کنند.
مشاهده بیشتر
تبلیغات ما
مشتریان به طور فزاینده ای آنلاین هستند. تبلیغات می تواند به آنها کمک کند تا کسب و کار شما را پیدا کنند.
مشاهده بیشتر
تبلیغات ما
مشتریان به طور فزاینده ای آنلاین هستند. تبلیغات می تواند به آنها کمک کند تا کسب و کار شما را پیدا کنند.
مشاهده بیشتر
تبلیغات ما
مشتریان به طور فزاینده ای آنلاین هستند. تبلیغات می تواند به آنها کمک کند تا کسب و کار شما را پیدا کنند.
مشاهده بیشترتوضیحات
Bayesian models for football leagues
| ویژگی | مقدار |
|---|---|
| سیستم عامل | - |
| نام فایل | bpl-0.1.1 |
| نام | bpl |
| نسخه کتابخانه | 0.1.1 |
| نگهدارنده | [] |
| ایمیل نگهدارنده | [] |
| نویسنده | Angus Williams <anguswilliams91@gmail.com> |
| ایمیل نویسنده | anguswilliams91@gmail.com |
| آدرس صفحه اصلی | https://github.com/anguswilliams91/bpl |
| آدرس اینترنتی | https://pypi.org/project/bpl/ |
| مجوز | GPL-3.0 |
# bpl
[](https://travis-ci.org/anguswilliams91/bpl)
[](https://codecov.io/gh/anguswilliams91/bpl)
[](https://pepy.tech/project/bpl)
`bpl` is a python 3 library for fitting Bayesian versions of the Dixon \& Coles (1997) model to data.
It uses the `stan` library to fit models to data.
## Installation
```bash
pip install bpl
```
## Usage
`bpl` provides a class `BPLModel` that can be used to forecast the outcome of football matches.
Data should be provided to the model as a `pandas` dataframe, with columns `home_team`, `away_team`, `home_goals` and `away_goals`.
You can also optionally provide a set of numerical covariates for each team (e.g. their ratings on FIFA) and these will be used in the fit.
Example usage:
```python
import bpl
import pandas as pd
df_train = pd.read_csv("<path-to-training-data>")
df_X = pd.read_csv("<path-to-team-level-covariates>")
forecaster = bpl.BPLModel(data=df_train, X=df_X)
forecaster.fit(seed=42)
# calculate the probability that team 1 beats team 2 3-0 at home:
forecaster.score_probability("Team 1", "Team 2", 3, 0)
# calculate the probabilities of a home win, an away win and a draw:
forecaster.overall_probabilities("Team 1", "Team 2")
# compute home win, away win and draw probabilities for a collection of matches:
df_test = pd.read_csv("<path-to-test-data>") # must have columns "home_team" and "away_team"
forecaster.predict_future_matches(df_test)
# add a new, previously unseen team to the model by sampling from the prior
X_3 = np.array([0.1, -0.5, 3.0]) # the covariates for the new team
forecaster.add_new_team("Team 3", X=X_3, seed=43)
```
## Statistical model
The statistical model behind `bpl` is a slight variation on the Dixon & Coles approach.
The likelihood is:
%20%3D%20\tau(y_h%2C%20y_a)\times%20\mathrm{Poisson}(y_h%20\%2C%20|%20\%2C%20a_h%20b_a%20\gamma_h)%20\times%20\mathrm{Poisson}(y_a%20\%2C%20|%20\%2C%20a_a%20b_h))
where y_h and y_a are the number of goals scored by the home team and the away team, respectively.
a_i is the *attacking aptitude* of team i and b_i is the *defending aptitude* of team j.
gamma_i represents the home advantage for team i, and tau is a correlation term that was introduced by Dixon and Coles to produce more realistic scorelines in low-scoring matches.
The model uses the following bivariate, hierarchical prior for a and b
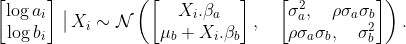
X_i are a set of (optional) team-level covariates (these could be, for example, the attack and defence ratings of team i on Fifa).
beta are coefficient vectors, and mu_b is an offset for the defence parameter.
rho encodes the correlation between a and b, since teams that are strong at attacking also tend to be strong at defending as well.
The home advantage has a log-normal prior
%2C)
Finally, the hyper-priors are
%2C%20\nonumber%20\\%20\sigma_a%2C%20\sigma_b%20%2C%20\sigma_\gamma%20%26\sim%20\mathcal{N}^+(0%2C%201)%2C%20\nonumber%20\\%20u%20%3D%20(\rho%20+%201)%20/%202%20%26\sim%20\mathrm{Beta}(2%2C%204).%20\nonumber%20\end{align})
نیازمندی
| مقدار | نام |
|---|---|
| >=0.22 | Cython |
| ~=2.19.1.1 | pystan |
| >=1.10.0 | numpy |
| >=0.20.1 | pandas |
| >=1.1.0 | scipy |
| >=4.25.0 | tqdm |
نحوه نصب
نصب پکیج whl bpl-0.1.1:
pip install bpl-0.1.1.whl
نصب پکیج tar.gz bpl-0.1.1:
pip install bpl-0.1.1.tar.gz