معرفی شرکت ها
benfords-1.0.2
تبلیغات ما
مشتریان به طور فزاینده ای آنلاین هستند. تبلیغات می تواند به آنها کمک کند تا کسب و کار شما را پیدا کنند.
مشاهده بیشتر
تبلیغات ما
مشتریان به طور فزاینده ای آنلاین هستند. تبلیغات می تواند به آنها کمک کند تا کسب و کار شما را پیدا کنند.
مشاهده بیشتر
تبلیغات ما
مشتریان به طور فزاینده ای آنلاین هستند. تبلیغات می تواند به آنها کمک کند تا کسب و کار شما را پیدا کنند.
مشاهده بیشتر
تبلیغات ما
مشتریان به طور فزاینده ای آنلاین هستند. تبلیغات می تواند به آنها کمک کند تا کسب و کار شما را پیدا کنند.
مشاهده بیشتر
تبلیغات ما
مشتریان به طور فزاینده ای آنلاین هستند. تبلیغات می تواند به آنها کمک کند تا کسب و کار شما را پیدا کنند.
مشاهده بیشترتوضیحات
Provides a series of functions to make Benford's Law usage more convenient.
| ویژگی | مقدار |
|---|---|
| سیستم عامل | - |
| نام فایل | benfords-1.0.2 |
| نام | benfords |
| نسخه کتابخانه | 1.0.2 |
| نگهدارنده | [] |
| ایمیل نگهدارنده | [] |
| نویسنده | Daniel McCarville |
| ایمیل نویسنده | daniel.mccarville@gmail.com |
| آدرس صفحه اصلی | https://github.com/danielmccarville/Benfords |
| آدرس اینترنتی | https://pypi.org/project/benfords/ |
| مجوز | - |
# Benfords
Benfords provides a series of functions intended to make Benford's Law research and usage more convenient.
## Usage
With Benfords you can conduct quick comparisons to Benfords law, create outputs like charts and .csv files, generate random Benford-variates, as well as calculate the expected probabilities or extract your own empirical digit frequencies.
### Comparisons to Benford's Law
The benfords() function allows you to quickly compare your data's digits to Benford's Law:
```python
import benfords
#Generate some random data
test_data = variate(1000)
#Compare to Benford's Law
benfords(test_data)
# Digit Expected Value Actual Value Difference
#0 1 0.301030 0.316 0.014970
#1 2 0.176091 0.178 0.001909
#2 3 0.124939 0.113 -0.011939
#3 4 0.096910 0.097 0.000090
#4 5 0.079181 0.075 -0.004181
#5 6 0.066947 0.072 0.005053
#6 7 0.057992 0.059 0.001008
#7 8 0.051153 0.041 -0.010153
#8 9 0.045757 0.049 0.003243
```
Use test() to calculate test statistics:
```python
test(benfords(test_data), test_statistic='d')
# 0.01914657325117365
```
Currently, test() supports only the d statistic described in [Cho and Gaines, 2012](http://cho.pol.illinois.edu/wendy/papers/bentas.pdf). Future releases will include additional test statistics.
benfords() can also output charts and csv:
```python
benfords(test_data, output_csv=True, output_plot=True, filename='2021-01-31 Analysis')
```
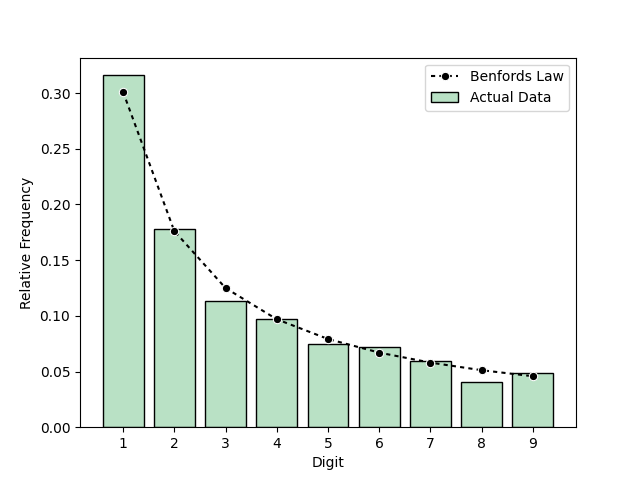
There are also parmeters for examining the digits beyond the first, as well as multiple digits at a time. This example uses the second and third digits:
```python
benfords(test_data, start_position=2, length=2)
# Digit Expected Value Actual Value Difference
#0 0 0.119679 0.000 -0.119679
#1 1 0.113890 0.000 -0.113890
#2 2 0.108821 0.000 -0.108821
#3 3 0.104330 0.000 -0.104330
#4 4 0.100308 0.000 -0.100308
#.. ... ... ... ...
#95 95 0.027760 0.002 -0.025760
#96 96 0.027558 0.009 -0.018558
#97 97 0.027358 0.005 -0.022358
#98 98 0.027162 0.004 -0.023162
#99 99 0.026969 0.007 -0.019969
#
#[100 rows x 4 columns]
```
### Generate random Benford-distributed digits.
You can generate random Benford-distributed digits with the variate() function. Just specify how many you want:
```python
variate(5)
# [6.494198781949683, 5.511615661880242, 7.311726835973362, 1.6809486480388234, 8.877345103827716]
```
Variates are generated according to the method in [Jamain, 2001](http://wwwf.imperial.ac.uk/~nadams/classificationgroup/Benfords-Law.pdf).
### Expected Probabilities
Calculate the probabilities expected under Benford's Law with expectation(). What's the expected probability that the second digit will be 5?
```python
expectation(5, 2)
# 0.09667723580232242
```
### Extract the significant digits from your data
fsd() and nsd() return the significant digits of your input data. They currently enjoy scalars (integers and floats), lists, 1d numpy arrays, and pandas dataframes.
fsd() returns the first significant digit according to the significand formula provided by [Berger and Hill, 2015](https://press.princeton.edu/books/hardcover/9780691163062/an-introduction-to-benfords-law).
```python
test = [5, 0.321, -2989.2, -0.00001]
fsd(test)
#array([5., 3., 2., 1.])
```
#NSD() returns the nth digit of your data. It always returns a numpy array containing strings. It includes parameters to select the second, third, and higher digits, as well as control the number of digits. This example shows the 4th significant digits.
```python
nsd(test, 4)
#array(['0', '1', '8', '0']
```
## Citation
If you use this work in your own research, please cite it in your publications:
```
McCarville, Daniel. Benford's Law, (2021). https://github.com/danielmccarville/Benfords
```
## License
[MIT](https://choosealicense.com/licenses/mit/)
زبان مورد نیاز
| مقدار | نام |
|---|---|
| >=3.6 | Python |
نحوه نصب
نصب پکیج whl benfords-1.0.2:
pip install benfords-1.0.2.whl
نصب پکیج tar.gz benfords-1.0.2:
pip install benfords-1.0.2.tar.gz